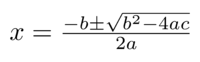From Prog0

演習第13回

1 演習問題
- 1.1 出席確認
2 A問題
- 2.1 A-1 キューのプログラム
- 2.2 A-2 情報落ちの実験
3 B問題
- 3.1 B-1 スタックのプログラム（検索機能）
- 3.2 B-2 数値計算の誤差について
4 Extra問題
- 4.1 E-1 空気抵抗を考慮した落下運動
5 課題提出上の注意事項

演習問題

主な内容

スタック
キュー
数値計算と誤差

以下の問題を解いて期限内に解答を提出してください。

なお、一人ひとりの授業理解度を確認することを目的として、口頭試問形式による採点を行います。
採点対象の問題が解けたら手を挙げ、教員またはTA/SAを呼んでください。口頭で解答の内容を説明してもらいます。
正しく説明できた場合は点数を付け、説明が不十分な場合はやり直してもらいます（間違えても減点はしません）。
今回の口頭採点の対象は A-1 の1問のみです。
(口頭採点の対象も、その他の問題と同様、menuコマンドで提出してください。)

出席確認

演習時間中に出席確認をLMS上の「演習出欠」で行ってください。出席確認用のパスワードは演習時間のどこかのタイミングで提示されます。

A問題

A-1 キューのプログラム

ファイル名: ex13a1.c

1. ハンドアウトの例題 lec13-2b.c を自分のディレクトリにコピーし、実行して動作を理解してください。

% cp /home/course/prog0/public_html/2025/lec/source/lec13-2b.c .

2. これをもとに、以下のような変更を加えて、実行例のように動作するプログラムを書いてください。

キューがいっぱいかどうかをチェックする関数 isFull() を作成する。
- 引数は無し。戻り値は int型。
- キューがいっぱいなら 1 を、空きがあれば 0 を返す。
キューが空かどうかをチェックする関数 isEmpty() を作成する。
- 引数は無し。戻り値は int型。
- キューが空なら 1 を、データが一つでもあれば 0 を返す。
enqueue()関数内のキューがいっぱいでないことのチェックと、dequeue関数内のキューが空でないことのチェックを、作成した isFull()関数、isEmpty()関数を使う形に変更する。
- これに伴い、不要な変数を減らす等の変更をしてもよい。

[実行例]

% ./a.out
input>> 2
  [Queue] 2
input>> 4
  [Queue] 2 4
input>> 6
  [Queue] 2 4 6
input>> 10
  [Queue] 2 4 6 10
input>> 0
Data: 2
  [Queue] 4 6 10
input>> 0
Data: 4
  [Queue] 6 10
input>> 0
Data: 6
  [Queue] 10
input>> 0
Data: 10
  [Queue]
input>> 0
Queue is empty!
%

A-2 情報落ちの実験

ファイル名: ex13a2.c

下記のコードは ∑ 1/n² = 1 + 1/4 + 1/9 + 1/16 + .....
を n=1 から指定した項数まで計算して表示するプログラムである。

プログラム

#include <stdio.h>

int main(){
  double x, s;
  int n, nmax;

  printf("何項計算しますか？: ");
  scanf("%d", &nmax);   /* 注：int型使用のため2147483646が限界 */

  s = 0.0;
  for( n=1; n<=nmax; n++ ){
    x = (double)n;
    s += 1.0/(x*x);
  }
  printf("1/n^2の総和: %.14f\n", s);
  return 0;
}

実行例

% ./a.out
何項計算しますか？: 2
1/n^2の総和: 1.25000000000000
% ./a.out
何項計算しますか？: 1000
1/n^2の総和: 1.64393456668156
%

∑ 1/n² は、和をとる項数をどんどん増やしていくと、総和はしだいに増えていき π²/6 = 1.644934066848226..... という収束値に近づくはずなのだが、上のプログラムでは項数を大きくしていくと、ある値から先は増加が止まってしまうようだ。

上記のプログラムを実行して、大体どのくらいの項数で結果が増えなくなるか調べてみなさい（計算に時間が掛かるので、最大でも10億項以下でよい）。結果はメモしておくこと。
「情報落ち」による誤差が減るようにプログラムを修正し、修正したプログラムを実行して元のプログラムより先まで結果が増え続けることを確認しなさい。
確認できたら、修正したプログラムを提出してください。

B問題

B-1 スタックのプログラム（検索機能）

ファイル名: ex13b1.c

ハンドアウトの例題 lec13-1b.c を参考に、以下のような仕様で、スタックの動作を試すプログラムを書きなさい。

スタックに格納するデータは int型で、最大100個まで格納できることとする（lec13-1b.cに実装済み）
スタックに対する操作はキーボードから整数を入力することで指示する。スタックの操作は無限ループで繰り返す。
- 正の整数が入力されたら、それをスタックに挿入(push)する。
- 負の整数が入力されたら、スタックからデータを一つ取り出して表示(pop)を行う。
- 0 が入力されたら、検索したい値（検索値）の入力を促す。そして、
  - 検索値がスタック中に存在するか調べ、あればスタック中の位置を含めてメッセージを表示する。
  - 無ければ無い旨のメッセージを表示する（実行例参照）。二つ以上存在するかは調べなくてよい。

次のいずれかの場合はエラーとなり、プログラムを終了する
- pop()時にスタックが空（lec13-1b.cに実装済み）
- push()時にスタックがいっぱい（lec13-1b.cに実装済み）
- 検索時に検索値がスタック中に存在しない（実行例参照）

実行例

% ./a.out
--- Input [+] to push, [-] to pop, [0] to detect --- >> 10
  [Stack] 10

--- Input [+] to push, [-] to pop, [0] to detect --- >> 20
  [Stack] 10 20

--- Input [+] to push, [-] to pop, [0] to detect --- >> 30
  [Stack] 10 20 30

--- Input [+] to push, [-] to pop, [0] to detect --- >> 40
  [Stack] 10 20 30 40

--- Input [+] to push, [-] to pop, [0] to detect --- >> -8
Data: 40
  [Stack] 10 20 30

--- Input [+] to push, [-] to pop, [0] to detect --- >> -9
Data: 30
  [Stack] 10 20

--- Input [+] to push, [-] to pop, [0] to detect --- >> 0
Detect what ? :20
20 exists at stack[1]
  [Stack] 10 20

--- Input [+] to push, [-] to pop, [0] to detect --- >> 0
Detect what ? :44
44 not in stack!
%

B-2 数値計算の誤差について

ファイル名: ex13b2.c

背　景

変数xについての二次方程式

a x² + b x + c = 0

(a≠0)は、解が2つあり、以下の式で計算できる。

しかし、もし方程式の定数a, b, cの値が、b >> ac (bの値がaとcの積より非常に大きい)となる場合、２つの解のうち片方は、誤差が大きくなってしまう。
なぜなら、解の式の分子の平方根の、複号のプラス側の計算のとき、分子はほぼ -b+b の非常に小さい値となり、浮動小数点演算の誤差が大きくなるためである。
例えば、 a = 1.01, b = 2718281.0, c = 0.01 のような場合に、そうした状況が起こるだろう。

この問題では、そのような誤差を実際に計算し、数値計算において誤差が問題となる状況を体験してみよう。

問　い

上の式で解を計算する関数のプロトタイプを、以下のように定義する。

double solve_qudratic(double a, double b, double c, int sel);

引数a, b, cは、二次方程式の定数に対応する。
4つ目の引数selは、分子の平方根の複号（±）の選択に使い、

1の場合には複号の＋を選択、
1以外の場合には複号のーを選択

するものとする。

定数が a = 1.01, b = 2718281.0, c = 0.01 の場合に、

関数solve_qudraticで2つの数値解を1つずつ計算して、
それぞれの相対誤差(真の解から数値解がずれている割合)を求めて出力

するプログラムを作成しなさい。

相対誤差は、以下の式で計算できる。

数値解の相対誤差　＝ |真の解 - 数値解| / |真の解|

この「真の解」として、次の値を利用のこと。

x₁ = -2691367.32673266

x₂ = -3.6787955329121653e-9

なお、平方根を計算する関数double sqrt(double)と、絶対値を計算する関数double fabs(double)を利用して良い。

プログラムのテンプレート

#include <stdio.h>
#include <math.h>

double x1 = -2691367.32673266;
double x2 = -3.6787955329121653e-9;

double solve_qudratic(double a, double b, double c, int sel) { 

    /* selの値に応じて、二次方程式の解を1つ返す関数 */

}
 
int main() { 

    /* solve_qudratic()で2つの解を１つずつ求め、
       それぞれ相対誤差を求めて出力する処理  */

  return 0;
}

この例では、x2側の相対誤差が大きく、x1側の相対誤差が小さく表示されるだろう。

Extra問題

E-1 空気抵抗を考慮した落下運動

ファイル名: ex13e1.c

ハンドアウトでは、質点の自由落下の問題の数値計算法を扱った。

現実には空気抵抗によって減速されるので、落下速度はもっと遅くなりうる。速度が遅く小さい物体の場合には「粘性抵抗」と呼ばれる速度の大きさに比例した抵抗力がかかり、速度が速く大きい物体には「慣性抵抗」と呼ばれる速度の2乗に比例した抵抗力がかかる。ここでは、粘性抵抗を考慮した場合の落下運動を計算してみよう。

速度 v でゆっくり動いている半径 a の球に働く粘性抵抗力は、速度と逆の向きに

となる。ここで、空気の粘性係数（単位はSI単位系で、長さ m, 質量 kg, 時間 s 等である）

したがって、重力と空気抵抗を考えた時の運動方程式は、質量を m 、重力加速度を g として

となる。

では、上記の空気抵抗を考慮した運動方程式を用いて、球状の物体が重力で落下する時に時間、位置、速度がどのように変化していくか計算するプログラムを以下の仕様で作成しなさい。

下にプログラムの一部（キーボード入力までの部分）を示すので、これに必要なコードを追加していくと良い。重力加速度と粘性係数はマクロで与えてある。また、計算タイムステップ dt （ハンドアウトの変数 h に対応）は小さくしないと正常に計算が行えないことがあるので、0.00001 にしてある。
初期状態の速度（m/s）、位置（m）、計算を行う時間（秒）、物体の半径（m）、質量（kg）はキーボードからの入力で与える（実行例参照）。
時間変化の計算は、ハンドアウトと同様に、オイラー法を使った繰り返し計算を行えばよい。速度を計算する部分を上記の運動方程式に合わせて修正すること。
ハンドアウトと異なり、時刻 t がキーボードから入力した秒数に達したら終了とする。
タイムステップが小さいので、毎回結果表示するのでは出力が多すぎる。そこで、出力すべき時間間隔もキーボード入力で与える（実行例参照）。出力は毎回ではなく、指定した時間が経過するごとに時刻、位置、速度を1行に出力する。（浮動小数点数の丸め誤差を考慮しないと思い通りの出力にならない可能性があるので注意）

なお、物体としては、半径 0.001 mm～0.05 mm (1 x 10^-6 ～ 5 x 10^-5 m) 程度の水滴（雲や霧の粒くらい）を想定する（これ以上重くなると、慣性抵抗も考慮する必要が出てくる）。実行時に質量を入力する必要があるが、水滴の質量は、半径 0.001 mm で 4.2 x 10^-15 kg、半径 0.01 mm では 4.2 x 10^-12 kg、半径 0.05 mm では 0.52 x 10^-9 kg である。

[プログラム例]

#include <stdio.h>

#define G  9.80     /* 重力加速度 */
#define VISC 1.8e-5 /* 空気の粘性係数 */

int main (){
  double v, x, t=0.0, tmax, a, m, c_m;
  double dt=0.00001;     /* タイムステップの値（十分小さくとること） */
  double dtp;
  double pi = 3.14159265358979; /* 円周率 */
  /* 必要な変数宣言を追加すること */


  printf("初期状態の速度、位置と、計算する時間を入力してください\n");
  scanf( "%lg%lg%lg", &v, &x, &tmax );
  printf("物体の半径と質量を入力してください\n");
  scanf( "%lg%lg", &a, &m );

  printf("出力の間隔を入力してください: ");
  scanf("%lg", &dtp);
  if (dtp < dt) dtp = dt; /* おかしな入力は修正 */

  ..... 続きを作成 .....

[実行例]

% ./a.out
初期状態の速度、位置と、計算する時間を入力してください
0 0 1
物体の半径と質量を入力してください
5e-5 0.52e-9             ←半径 0.05 mm の例
出力の間隔を入力してください: 0.02
    時間     位置     速度
  0.0000   0.0000   0.0000
  0.0200  -0.0016  -0.1440
  0.0400  -0.0053  -0.2189
  0.0600  -0.0101  -0.2580
  0.0800  -0.0155  -0.2783
  0.1000  -0.0212  -0.2889
  ...
  0.9600  -0.2792  -0.3004
  0.9800  -0.2852  -0.3004
  1.0000  -0.2912  -0.3004     ←下向き約 30 cm/s で落下
% ./a.out
初期状態の速度、位置と、計算する時間を入力してください
0 0 0.5
物体の半径と質量を入力してください
1e-5 4.2e-12             ←半径 0.01 mm の例
出力の間隔を入力してください: 0.05
    時間     位置     速度
  0.0000   0.0000   0.0000
  0.0500  -0.0006  -0.0121
  0.1000  -0.0012  -0.0121
  0.1500  -0.0018  -0.0121
  0.2000  -0.0024  -0.0121
  0.2500  -0.0030  -0.0121
  0.3000  -0.0036  -0.0121
  0.3500  -0.0042  -0.0121
  0.4000  -0.0048  -0.0121
  0.4500  -0.0054  -0.0121
  0.5000  -0.0061  -0.0121     ←下向き約 1.2 cm/s で落下
%

この結果から、粒子が小さくなるにつれて落下速度は極めてゆっくりになり、しかもごく短時間で重力と空気抵抗が釣り合って速度が一定になることが分かる。空気抵抗のため、雲をつくっている水滴や、細かい塵、黄砂、PM2.5のような非常に小さく軽い物体は、空気中ではなかなか落ちてこない。

課題提出上の注意事項

解答ファイルはmenuコマンドを使って提出してください。以下のようにmenuコマンドを実行し、表示されるメッセージに沿って操作すること。

% ~prog0/bin/menu

menuコマンドは、解答ファイルが ~/Prog0/Ex## のディレクトリに指定されたファイル名で置かれているものとして処理します。正常に提出された場合は ○ が、何らかのエラーが生じた場合は × が表示されます。

解答の提出期間は以下のとおりです。

問題	提出受付開始	提出〆切
A問題	演習日の6日前の午後9時	演習終了時刻
B, Extra問題	演習日の6日前の午後9時	演習日の6日後の午後9時

提出は〆切前であれば何度でもやり直すことができます。再提出すると、前に提出したファイルは新しい内容で上書きされます。

Ex13

From Prog0

Contents

演習問題

出席確認

A問題

A-1 キューのプログラム

A-2 情報落ちの実験

B問題

B-1 スタックのプログラム（検索機能）

B-2 数値計算の誤差について

Extra問題

E-1 空気抵抗を考慮した落下運動

課題提出上の注意事項

Views

Personal tools

Navigation

Search

Toolbox