Ex08
From Prog0
演習第8回
Contents |
演習問題
主な内容
- フローチャート
これまでの課題において、「理由はよく分からないけれど、試行錯誤しているうちにそれらしいプログラムができてしまった」という人もいるのではないでしょうか。しかし、そのようなやり方でプログラムを書く習慣が身についてしまうと、簡単な課題でも余計に時間がかかったり、複雑なプログラムではまったく手が出せなくなったりするおそれがあります。そうならないようにするためには、与えられた問題をよく分析し、どのようなプログラムを書くべきかを考え、設計を行うことが重要です。今回は、その練習としてフローチャートを活用したプログラミングに取り組みます。
今回は、口頭採点の対象となる問題はありません。すべての問題について、menuコマンドを使用してファイルを提出してください。
出席確認
演習時間中に出席確認をLMS上の「演習出欠」で行ってください。出席確認用のパスワードは演習時間のどこかのタイミングで提示されます。
参考資料
A問題
A-1 つるかめむし算問題の再定義
ファイル名: ex08a1.txt
つるかめ算問題の再定義の例にならって、以下の「つるかめむし算問題」を再定義し、その内容を ex08a1.txt に記述しなさい。
[つるかめむし算問題]
鶴と亀とてんとう虫が合わせて 20 いて、足の合計本数が ashi_total 本である。鶴、亀、てんとう虫はそれぞれ何羽・匹いるか?
[再定義]
- 与えられた問題を分析して問題を再定義する。
- 与えられた情報は何か
- 与えられていないが常識として知っている情報は何か
- 求めるものは何か
A-2 つるかめむし算問題のフローチャートの作成
ファイル名: ex08a2.pdf
「つるかめむし算問題」の再定義をもとに、条件を満たすすべての答えを表示して終了する処理を示すフローチャートを作成しなさい。ただし、条件を満たす答えが存在しない場合は「NOT found!」と表示すること。また、足の合計本数(ashi_total)の値は、プログラム実行時にキーボードから入力されるものとする。
フローチャートの作成には、以下に示すいずれかのツールを用いること。
- diagrams.net(旧draw.io)
- OpenOffice Draw
- その他 PowerPoint など同等の作図機能を持つツール
diagrams.net を使用したフローチャートの作成については 別ページの解説 を参照のこと。
作成したフローチャートは ex08a2.pdf という名前のPDFで書き出して提出すること。
B問題
B-1 つるかめむし算問題のプログラムの作成
ファイル名: ex08b1.c
作成した「つるかめむし算問題」のフローチャートに沿ってプログラムを作成しなさい。
実行例は以下の通り(カッコ内は足の本数)であるが、書式は例と異なっていてもよい。
[実行例]
% ./a.out
Input ashi (total): 88
Turu:0(0) Kame:16(64) Tentoumushi:4(24)
Turu:1(2) Kame:14(56) Tentoumushi:5(30)
Turu:2(4) Kame:12(48) Tentoumushi:6(36)
Turu:3(6) Kame:10(40) Tentoumushi:7(42)
Turu:4(8) Kame:8(32) Tentoumushi:8(48)
Turu:5(10) Kame:6(24) Tentoumushi:9(54)
Turu:6(12) Kame:4(16) Tentoumushi:10(60)
Turu:7(14) Kame:2(8) Tentoumushi:11(66)
Turu:8(16) Kame:0(0) Tentoumushi:12(72)
% ./a.out
Input ashi (total): 116
Turu:0(0) Kame:2(8) Tentoumushi:18(108)
Turu:1(2) Kame:0(0) Tentoumushi:19(114)
% ./a.out
Input ashi (total): 99
NOT found!
%
B-2 フィボナッチ数列
ファイル名: ex08b2.c
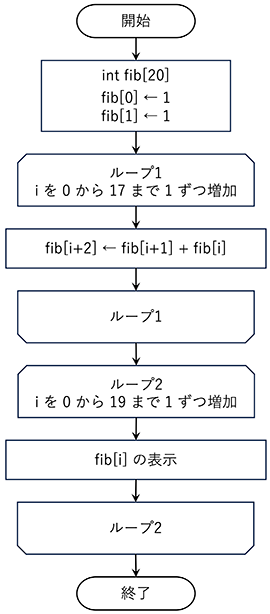
以下のフローチャートと実行例を参考にして、n = 20 までのフィボナッチ数列を表示するプログラムを作成しなさい。フィボナッチ数列とは、次の漸化式で表される数列である。
F1 = 1 F2 = 1 Fn = Fn-1 + Fn-2
[フローチャート]
[実行例]
% ./a.out
1
1
2
3
5
8
13
21
34
55
89
144
233
377
610
987
1597
2584
4181
6765
%
B-3 完全数
ファイル名: ex08b3.c
完全数とは、自分自身を除くすべての約数の和がその数自身と等しくなるような数のことである。たとえば、
6 = 1 + 2 + 3 28 = 1 + 2 + 4 + 7 + 14
となることから、6と28は完全数である。10,000以下の完全数は、6、28、496、8128の4つのみである。このことを実際に計算によって確認するためのプログラムを作成したい。
- このプログラムのフローチャートを作成しなさい。
- 作成したフローチャートに基づいて、実際にプログラムを作成しなさい。
10,000以下の完全数を求めるには、1から10,000までのすべての整数 n に対して、次の処理を行えばよい。
- 1 から n/2 までのすべての整数 d について、d が n の約数かどうかを調べる。約数かどうかは、n を d で割ったときに余りが出るかどうかで判断できる。
- d が約数であれば、その値を「約数の和」を保持する変数に加える。
- すべての約数を加算し終えた後、約数の和が n と等しければ、n を完全数として出力する。
[実行例]
% ./a.out
6 は完全数です
28 は完全数です
496 は完全数です
8128 は完全数です
%
課題提出上の注意事項
解答ファイルはmenuコマンドを使って提出してください。以下のようにmenuコマンドを実行し、表示されるメッセージに沿って操作すること。
% ~prog0/bin/menu
menuコマンドは、解答ファイルが ~/Prog0/Ex## のディレクトリに指定されたファイル名で置かれているものとして処理します。正常に提出された場合は ○ が、何らかのエラーが生じた場合は × が表示されます。
解答の提出期間は以下のとおりです。
| 問題 | 提出受付開始 | 提出〆切 |
|---|---|---|
| A問題 | 演習日の6日前の午後9時 | 演習終了時刻 |
| B, Extra問題 | 演習日の6日前の午後9時 | 演習日の6日後の午後9時 |
提出は〆切前であれば何度でもやり直すことができます。再提出すると、前に提出したファイルは新しい内容で上書きされます。