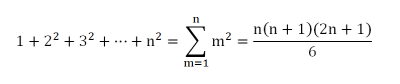Ex06
From Prog0
演習第6回
Contents |
演習問題
主な内容
- forループ
- break/continue
以下の問題を解いて期限内に解答を提出してください。
一人ひとりの授業理解度を確認することを目的として、口頭試問形式による採点を行います。
採点対象の問題が解けたら手を挙げ、教員またはTA/SAを呼んでください。口頭で解答の内容を説明してもらいます。
正しく説明できた場合は点数を付け、説明が不十分な場合はやり直してもらいます(間違えても減点はしません)。
今回の口頭採点の対象は A-2 の1問のみです。
(口頭採点の対象も、その他の問題と同様、menuコマンドで提出してください。)
出席確認
演習時間中に出席確認をLMS上の「演習出欠」で行ってください。出席確認用のパスワードは演習時間のどこかのタイミングで提示されます。
A問題
A-1 5の倍数の和の計算
ファイル名: ex06a1.c
下のプログラムは、キーボードから読み込んだ整数以下で、5の倍数となるすべての正の整数の和を計算するものです。 for文中の (初期化;条件式;カウンター変数の更新) をそれぞれ適切な式に修正し、プログラムを完成させなさい。
#include <stdio.h>
int main()
{
int n, sum = 0;
int i;
printf("整数を入力して下さい:");
scanf("%d", &n);
for(初期化; 条件式; カウンター変数の更新){
if( i%5 == 0 ) {
sum += i ;
}
}
printf("%d以下で5の倍数となる正の整数の和は%dです\n", n, sum);
return 0;
}
[実行例]
% ./a.out
整数を入力して下さい: 26
26以下で5の倍数となる正の整数の和は75です
%
A-2 (口頭試問) break, continueの利用
ファイル名: ex06a2.c
ある試験の点数のリストがあるとする。試験の点数は0点から100点とする。点数のリストをキーボードから読み込み、決まった範囲にある答案の枚数をカウントしたい。 以下のプログラムで足りない部分を補ってプログラムを完成させなさい。
- カウントする点数の範囲は50点(変数"L")以上、80点(変数"U")未満とする。この場合に該当する答案の枚数をカウントする。
- カウントする変数は"count"とすること。
- continue文, break文を使うこと。
- 負の数が入力されたら、ループを終了すること。
- forループ内の「必要な処理」以外の部分を変更してはいけない。
#include <stdio.h>
int main()
{
int i;
int count;
int score;
int L = 50;
int U = 80;
count = 0;
printf("点数を入力して下さい\n");
for(i = 0; i < 15; i++){
scanf("%d", &score);
/* この部分に必要な処理を追加してください */
count++;
}
printf("%d点以上、%d点未満の答案の数は%dです\n", L, U, count);
return 0;
}
実行例
% ./a.out
点数を入力して下さい
51
-1
50点以上、80点未満の答案の数は1です
% ./a.out
点数を入力して下さい
10
20
30
-1
50点以上、80点未満の答案の数は0です
% ./a.out
点数を入力して下さい
33
55
83
92
60
-1
50点以上、80点未満の答案の数は2です
B問題
B-1 for, continue, breakを使った数当てゲーム
ファイル名: ex06b1.c
下のプログラムは、forループを使った数当てゲームである。 ルールは以下の通り。
- まず、正解の数をプログラムの中で指定しておく(下のプログラムでは47)。
- 挑戦者は、1から9までの数を10回入力することができる。同じ数を何度入力してもよい。
- 10回以内に、入力された数の合計が、プログラム内で指定されていた数と等しくなれば勝ち。
- 指定された数より、入力した数の合計のほうが大きくなってしまったら、その時点で終了。
- もし間違って10以上の数を入力したり、0以下の数を入力すると、回数だけをカウントする。
このプログラムで下線になっている部分を埋め、上のルールを満たすプログラムを完成しなさい。完成したら、下の実行例を参考にして、実際に正しく動作することを確認しなさい。最初に指定する数を変えてみて、いろいろ実行してみるのもよいでしょう。
#include <stdio.h>
int main()
{
int i, n, sum = 0;
int target = 47; /* この数を当てる */
int hit = 0; /* 当たったかどうか記録する変数(当たれば 1 にする) */
for( i=1 ; _____ ; _____ ) {
printf( "1から9までの数を入力して下さい。%2d回目: ", i );
scanf( "%d", &n );
/* 指定された範囲外の数が入力されたら、入力をやり直す(回数のカウントは増える) */
if( n>=10 || n<=0 ){
printf( "その数字は範囲外です\n" );
______________;
}
sum += n;
if( _____ == target ) { /* 当たりの判定 */
hit = 1;
__________;
}
if( _____ > target ) __________; /* 超過の判定 */
}
if( _____ == 1 ) printf( "%d回目で当たりました!\n\n", i );
else if( ______________ ) printf( "残念ですが、入力された数の合計(%d)が設定値未満でした。\n\n", _____ );
else printf( "残念ですが、入力された数の合計(%d)が設定値を超えました。\n\n", _____ );
return 0;
}
実行例
% ./a.out 1から9までの数を入力して下さい。 1回目: 7 1から9までの数を入力して下さい。 2回目: 8 1から9までの数を入力して下さい。 3回目: 9 1から9までの数を入力して下さい。 4回目: 10 その数字は範囲外です 1から9までの数を入力して下さい。 5回目: 9 1から9までの数を入力して下さい。 6回目: 6 1から9までの数を入力して下さい。 7回目: 3 1から9までの数を入力して下さい。 8回目: 5 8回目で当たりました! % ./a.out 1から9までの数を入力して下さい。 1回目: 9 1から9までの数を入力して下さい。 2回目: 8 1から9までの数を入力して下さい。 3回目: 7 1から9までの数を入力して下さい。 4回目: 6 1から9までの数を入力して下さい。 5回目: 5 1から9までの数を入力して下さい。 6回目: 4 1から9までの数を入力して下さい。 7回目: 3 1から9までの数を入力して下さい。 8回目: 2 1から9までの数を入力して下さい。 9回目: 1 1から9までの数を入力して下さい。10回目: 1 残念ですが、入力された数の合計(46)が設定値未満でした。 % ./a.out 1から9までの数を入力して下さい。 1回目: 9 1から9までの数を入力して下さい。 2回目: 9 1から9までの数を入力して下さい。 3回目: 9 1から9までの数を入力して下さい。 4回目: 9 1から9までの数を入力して下さい。 5回目: 9 1から9までの数を入力して下さい。 6回目: 9 残念ですが、入力された数の合計(54)が設定値を超えました。 %
B-2 読みやすいプログラム、無駄のないプログラム
ファイル名: ex06b2.c
以下のプログラムは、正の整数の2乗の和を算出するものである。高校で習ったように、正の整数の2乗の数列の和は、
となる。この等式の両辺の値をそれぞれ計算し、両方の結果を表示するプログラムである。
このプログラムは実行例のように正しく動作するのだが、適度な空白やインデントがないためとても読みにくい。
また、int型変数が8つも宣言されているが、このプログラムではそれほどたくさんのint型変数を必要としない。
これらの点を改善するように以下のプログラムを書き直したプログラムを作成しなさい。また、 書き直したプログラムが正しく動作することを確認しなさい。すなわち、
- 空白や空行、インデントを入れ、見やすいプログラムに整形する。
- アルゴリズムや計算処理を見直し、不要な変数を削減する。
という処理を行った上で、以下の実行例を参考に、正しく動作することを確かめなさい。
#include <stdio.h>
int main()
{
int i,k,m,n,p,q,s=0,s2;
printf("nを入力して下さい:");
scanf("%d", &n);
for(i=1;i<=n;i++){k=i*i;
s=s+k; printf("%d",k); if (i == n) break;
printf("+");}
m=n+1;p=2*n+1;q=n*m*p;s2=q/6;
printf(" = %dです\n",s);
printf("公式による結果は%dです\n",s2);
return 0;
}
[実行例]
% ./a.out
nを入力して下さい:3
1+4+9 = 14です
公式による結果は14です
% ./a.out
nを入力して下さい:8
1+4+9+16+25+36+49+64 = 204です
公式による結果は204です
% ./a.out
nを入力して下さい:18
1+4+9+16+25+36+49+64+81+100+121+144+169+196+225+256+289+324 = 2109です
公式による結果は2109です
%
B-3 アスキーアート
ファイル名: ex06b3.c
1〜9 までの値の整数 n を入力として受け取り、以下の実行例のように、その n を高さとした二等辺三角形を出力するプログラムを作成しなさい。なお、0以下か10以上が入力されたら実行例のようなエラーメッセージを表示するようにしなさい。
ただし、数字は変数をうまく使って繰り返し表示を行うこと。printf( "333\n" ); などのように直接 " " の中に数字の並びを書いて表示させるのは不可とする。
% ./a.out
1から9までの整数を入力してください:3
1
22
333
22
1
% ./a.out
1から9までの整数を入力してください:1
1
% ./a.out
1から9までの整数を入力してください:6
1
22
333
4444
55555
666666
55555
4444
333
22
1
% ./a.out
1から9までの整数を入力してください:11
入力する数は1から9までです
%
ヒント:行ごとに数字が変わっていく繰り返しがある一方、一つの行の中にも同じ数字を表示する繰り返しがあることに注意して for ループを組み合わせるとよい。
Extra問題
E-1 素数判定
ファイル名: ex06e1.c
以下の仕様に従ってプログラムを作成しなさい。
- for ループを使って、整数の入力を5回行う。
- それぞれの入力された整数について、それが素数がどうかを for ループを使って判定する。
- ただし、入力された整数が負の数, 0, 1 の場合には素数判定をしない。
- 素数判定のアルゴリズムは「整数 n について、 2 から n-1 までの全ての整数で割り切れない場合、n は素数と判定」とする。
- 実行例のように、全入力終了後に素数の総数を出力すること。
[実行例1]
% ./a.out
1個目の整数を入力してください:-1
入力は正の整数にしてください
2個目の整数を入力してください:1
入力された整数が 1 なのでスキップします
3個目の整数を入力してください:2
2 は素数
4個目の整数を入力してください:3
3 は素数
5個目の整数を入力してください:4
素数は 2 個ありました
%
[実行例2]
% ./a.out
1個目の整数を入力してください:51
2個目の整数を入力してください:53
53 は素数
3個目の整数を入力してください:55
4個目の整数を入力してください:57
5個目の整数を入力してください:59
59 は素数
素数は 2 個ありました
%
[実行例3]
% ./a.out
1個目の整数を入力してください:211
211 は素数
2個目の整数を入力してください:277
277 は素数
3個目の整数を入力してください:311
311 は素数
4個目の整数を入力してください:433
433 は素数
5個目の整数を入力してください:499
499 は素数
素数は 5 個ありました
%
課題提出上の注意事項
解答ファイルはmenuコマンドを使って提出してください。以下のようにmenuコマンドを実行し、表示されるメッセージに沿って操作すること。
% ~prog0/bin/menu
menuコマンドは、解答ファイルが ~/Prog0/Ex## のディレクトリに指定されたファイル名で置かれているものとして処理します。正常に提出された場合は ○ が、何らかのエラーが生じた場合は × が表示されます。
解答の提出期間は以下のとおりです。
| 問題 | 提出受付開始 | 提出〆切 |
|---|---|---|
| A問題 | 演習日の6日前の午後9時 | 演習終了時刻 |
| B, Extra問題 | 演習日の6日前の午後9時 | 演習日の6日後の午後9時 |
提出は〆切前であれば何度でもやり直すことができます。再提出すると、前に提出したファイルは新しい内容で上書きされます。