B問題

B-1 コラッツの問題

ファイル名: ex05b1.c

ドイツの数学者コラッツは任意の 0 でない自然数 n に対して、

• n が偶数の場合、n を 2 で割る
• n が奇数の場合、n に 3 をかけて 1 足す

という操作を繰り返すと、最終的に n は 1 になる、と予想した。これを コラッツの問題 と呼ぶ。 この問題はまだ証明はされていないものの、実際に任意の自然数 n に対してこの通りとなるか、コンピュータのプログラムで確かめることができる。

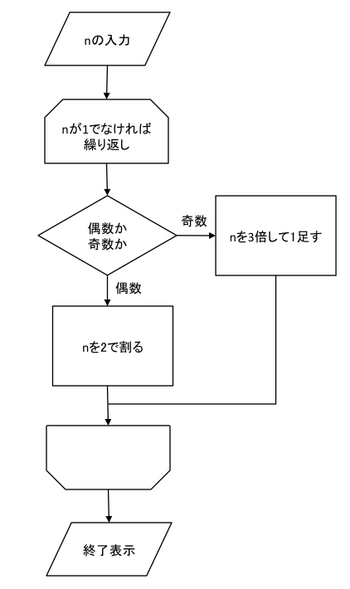
以下に示すフローチャートを参考にし、下線部および補うよう指示された部分を補ってプログラムを完成させなさい。

ただし、フローチャートには一部の画面表示の処理などは記入されていない。これらの処理についてはプログラム内で適切な場所を自分で考え、printf文などを入れること。

#include <stdio.h>

int main()
{
  int n;
  
  printf("0でない自然数nを入力して下さい ");
  scanf("%d", &n);
  
  while ( _______ ) {


  /* この部分に必要なプログラムを補う */    

   
  }

  printf("終了\n");
  return 0;   
}

[実行例]

% ./a.out
0でない自然数nを入力して下さい 3
n = 10
n = 5
n = 16
n = 8
n = 4
n = 2
n = 1
終了
%

B-2 コラッツの問題プログラムの改良

ファイル名: ex05b2.c

コラッツの問題で作成したプログラムに改良を加えて、以下のように計算の途中経過や計算回数がわかるようにしたい。

[実行例]

% ./a.out
0でない自然数nを入力
3
1回目
3は奇数
次の n = 10

2回目
10は偶数
次の n = 5

3回目
5は奇数
次の n = 16

4回目
16は偶数
次の n = 8

5回目
8は偶数
次の n = 4

6回目
4は偶数
次の n = 2

7回目
2は偶数
次の n = 1

7回目でn = 1 になりました

このプログラムを実現するためには、

• 計算回数を記録する変数の追加
• 毎回の n の状態（偶数か奇数か）を表示する機能の追加
• 次の n を表示する機能の追加
• 何回目で n=1 となったかを表示する機能の追加

が必要である。これらの機能追加を行い、プログラムを完成させよ。

B-3 ユークリッドの互除法

ファイル名: ex05b3.c

ユークリッドの互除法は、2 つの自然数（0を含むとする）の最大公約数を求める手法の一つである。アルゴリズム（手順）を以下に示す。

この方法を用いて、入力された二つの数値の最大公約数を求めるプログラムを作成しなさい。

ただし、実行例のように途中経過を表示すること。 入力値に対するエラー処理は含めなくてもよい。

　アルゴリズム

   1. 入力を m, n (m ≧ n) とする。
   2. n = 0 なら、 m を最大公約数として出力し、プログラムを終了する。
   3. m を n で割った余りを新たに n とし、
      元のnを新たにm として、
      2. に戻る。

[実行例]

% ./a.out
m nを入力して下さい：21 14
21 % 14 = 7
14 % 7 = 0
最大公約数は 7 です
% ./a.out
m nを入力して下さい：32 18
32 % 18 = 14
18 % 14 = 4
14 % 4 = 2
4 % 2 = 0
最大公約数は 2 です
% ./a.out
m nを入力して下さい：78 48
78 % 48 = 30
48 % 30 = 18
30 % 18 = 12
18 % 12 = 6
12 % 6 = 0
最大公約数は 6 です
%

B-4 インクリメント・デクリメント

ファイル名: ex05b4.txt

次のプログラムを作成し、実行せよ。

#include <stdio.h>

int main() {

    int i = 0;

    i++;
    printf("%d\n", i);
    ++i;
    printf("%d\n", i);
    printf("-------------\n");

    printf("%d\n", ++i);
    printf("%d\n", i++);
    printf("%d\n", --i);
    printf("%d\n", i--);

    return 0;
}

このプログラムの出力は以下の実行例のようになる。

[実行例]

% ./a.out    
1
2
-------------
3
3
3
3
%

"3"が連続して4回出力される理由を、 ex05b4.txt に簡潔に説明して提出してください。

説明の仕方は、下記にならってください。

最初の"3"は、前置インクリメントによって出力よりも前にiに1が足されるため、3が出力される。出力後のiの値は3である。
２番目の"3"は、・・・・・