Chromastereopsis; 色の立体視りったいし

“Double Rainbow”;「二重の虹にじゅうのにじ」, by Iwase Jiroh; 岩瀬 次郎

Wave tank

Waves bend (refract) when passing into media with different speeds of propagation. Waves also bend around obstacles (difract) and such bending depends upon the wave frequency.
Run the Ripple Tank simulator, by Paul Falstad.

• Choose “Example: Refraction” set-up (preset). The finite length line source (in top left of tank) creates wavefronts that have some shape between planes (for long generators) and circles (for point-shaped generators).
• Adjust the length of the source to confirm this. (Assert “Stopped” to pause the simulation, click “Clear Waves” to reset the simulation, move either end of the line source to shorten it [select the source by clicking it, then drag either end], and toggle “Stopped” to restart the simulation.)
• Observe bending of wave when passing from one medium to another. Pulses of a monotonic (single frequency) wave “pull into” medium of higher density (like tendency of vehicles to pull into rough gravel of road shoulder). Note that this phenomenon applies not only to visible light and near spectrum “light (UV [ultraviolet; 紫外線しがいせん] ↔ IR [infrared; 赤外線せきがいせん]”) phenomena, but also to sound, which is why acoustic waves bend into cooler air.
• Optional: enable 3-D View for projective perspective instead of orthographic display, inclding adjusting viewpoint by dragging display.
• Try the “Example: Single Slit”, “Example: Double Slit”, & “Example: Triple Slit” presets to observe how changing the source frequency changes the angles of difraction.

Refraction; 屈折くっせつ & Dispersion; 分散ぶんさん

The speed of light is not constant, but depends upon the medium through which it travels. The speed of light in air is almost the same as that in a vacuum, but the speed in glass is significantly slower. Further, speed depends upon frequency, with lower frequency (longer wavelengths) traveling slower than higher frequency (higher wavelengths). The refractive index is also equal to the velocity of light c of a given wavelength in empty space divided by its velocity v in a substance, or n = c/v.
This behavior is captured by Snell's Law: sin θ₂/sin θ₁ = v₂/v₁ = n₁/n₂, where θ₂ is the angle of incidence, θ₁ is the angle of refraction, v₂ is the speed of the wave in the incident medium, v₁ is the speed of the wave in the transmission medium, n₁=c/v₁ is the index of refraction of the incident medium, and n₂=c/v₂ is the index of refraction of the transmission medium.
Typical refractive indices for yellow light (wavelength equal to 589 nm [10⁻⁹ meter]) are the following:

• vacuum: 1.0000
• air: 1.0003
• water: 1.333
• crown glass: 1.517
• dense flint glass: 1.655
• diamond: 2.417.

The variation of refractive index with wavelength is the source of chromatic aberration in lenses. he refractive index of X-rays is slightly less than 1.0, which means that an X-ray entering a piece of glass from air will be bent away from the normal, unlike a ray of light, which will be bent toward the normal. [Ref.: Refractive index, Encyclopaedia Britannica]
Run the PhET “Bending Light”; 「光の屈折」demo (also available in other languages, including Mandarin Chinese, Traditional Chinese, ...)

• Choose first activity, “Intro.[duction]”;「光の屈折ひかりのくっせつ 」. Project light across media of different Indices of Refraction. Observe reflection and transmission, and conservation of energy such that total power is constant. (Use power meter to measure intensity of incident, reflected, and transmitted beams.) Use Snell’s Law to determine the Index of Refraction of “Mystery Material #1” and corresponding speed of light through that medium.
• 
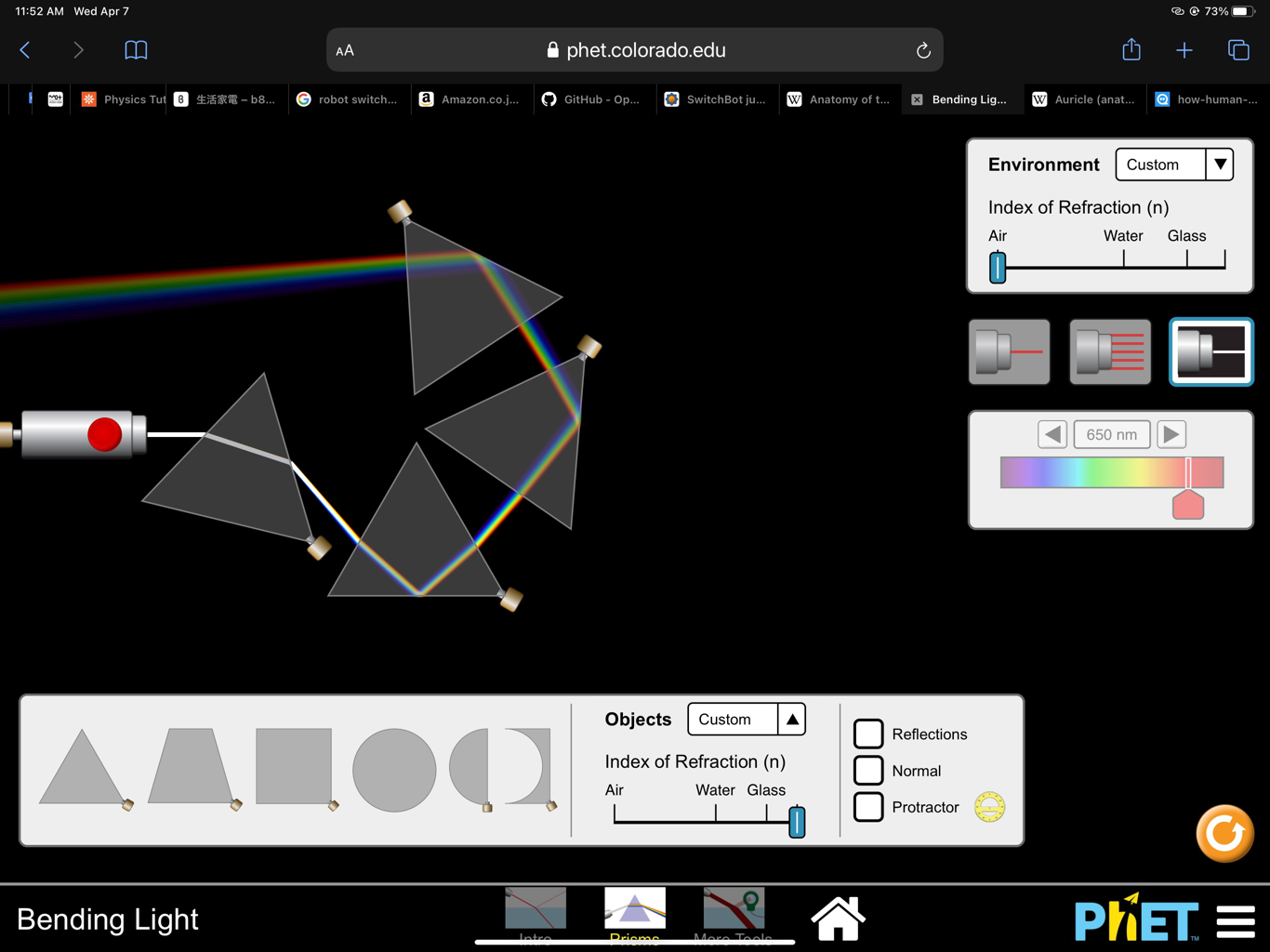
  Choose second activity, “Prisms”;「プリズム」. Arrange a triangular prism in front of monochromatic light source. Observe bending angle changing depending on frequency and wavelength due to refraction. Change light source to white light. Observe rainbow spectrum due to dispersion. Leaving the enviromental index of refraction at a minimum, maximize the index of refraction for the prism. Compose a series of prisms to broaden the rainbow.

Diffraction grating; 回折かいせつ格子こうし

Finallly, observe how a diffraction grating can act like a prism to cause dispersive refraction, thereby inducing color-coded binocular parallax for stereopsis, by running this simulation of a diffraction grating: oPhysics: Interactive Physics Simulation.

• Assert “Grating in Place” to simulate diffraction grating.
• Observe that changing the wavelength (and hence frequency) of the incident light changes the diffraction (bending) through the grating.

Reference links:

• Chromastereopsis
  • Chromatek & Chromastereopsis: Chromadepth 3D
  • Chromadepth 3D Design Guide
  • University of Aizu Exhibition ChromaDepth Picture Contest: E: 英語, J: 日本語
  • University of Aizu Chromadepth Picture Contest galleries
  • Wikipedia: ChromaDepth
  • OSU ChromaDepth Scientific Visualization Gallery
  • Brain Factory 3D chromadepth video (10 s.)
  • Michael Bailey & Dru Clark, “Using ChromaDepth to obtain Inexpensive Single-image Stereovision for Scientific Visualization,” J. of Graphics Tools, 3(3), Aug. 1999, pp. 1-9.
  • Chromostereopsis demo, Michael Bach
  • “Chromostereopsis: Advancing color and receding color,” Akitaoka Kitaoka; 北岡 明佳
  • Chromatic Depth Phenomena
  • 3-D Vision with ChromaDepth Glasses, by Christian Ucke, ICPE/GIREP (International Group on Physics Teaching) Conf. ‘Hands-On Experiments in Physics Education’ Aug., 1998, Duisburg, Germany, January 1999
• Photopea (online image editor) (link to bilingual version by Hoshino Yusui; 星野 結水)
• Color Vision; 光の色: Color Vision; 光の色
• How the Human Eye Works: Click (blue [off] ⥨ green [on]) the 360 ↺ icons to toggle inspection mode (rotatability).

maintained by Michael Cohen